サーミスタは金属酸化物を主原料とし高温にて焼結して得られるセラミック半導体で、その使用する材料によって様々な特性を得ることができます。
また用途に応じてサーミスタ素子を多種多様な形状に柔軟に加工ができることから、自動車や家電、医療といったあらゆる機器の温度測定や温度制御、温度補償等に使用する温度センサとして幅広く利用されています。
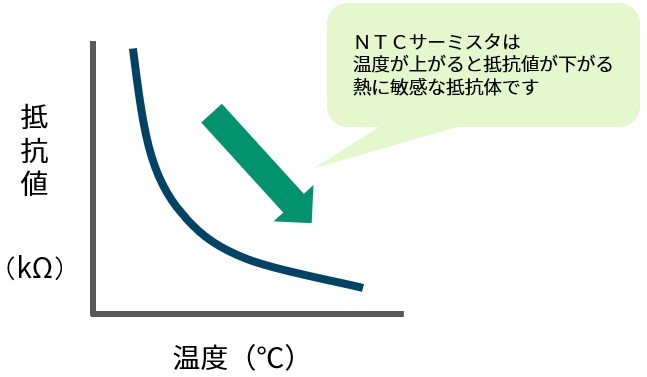
サーミスタとは、熱に敏感な抵抗体(Thermally Sensitive Resistor – Thermistor)の総称で、温度が変化することで抵抗値が大きく変化する半導体部品です。
温度が上がることで抵抗値が下がる(図1参照)、負の温度係数を有するものをNTCサーミスタ(Negative Temperature Coefficient Thermistor)と言います。
サーミスタは金属酸化物を主原料とし高温にて焼結して得られるセラミック半導体で、その使用する材料によって様々な特性を得ることができます。
また用途に応じてサーミスタ素子を多種多様な形状に柔軟に加工ができることから、自動車や家電、医療といったあらゆる機器の温度測定や温度制御、温度補償等に使用する温度センサとして幅広く利用されています。
サーミスタは温度で抵抗値が大きく変化しますが、図1にも示した通り、温度と抵抗値の関係は指数関数的に変化します。
サーミスタの温度特性は、ある温度範囲における抵抗値と温度の関係は、式1の様に近似的に表されます。
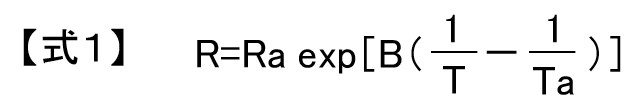
T、Ta: 絶対温度 (K)
R、Ra: T、Taにおけるゼロ負荷抵抗値 (Ω)
B :B定数 (K)
ゼロ負荷抵抗値とは、サーミスタは一定の温度で抵抗値を測定し、自己発熱による抵抗値変化が無視出来るような十分低い消費電力で測定した場合の抵抗値をゼロ負荷抵抗値といい「R25」の様に表記されます。R25であれば25℃の時のゼロ負荷抵抗値を示します。
B定数とは、抵抗一温度特性で任意の2点の温度から求めた抵抗値変化の大きさを表す定数で、式2によって表されます。
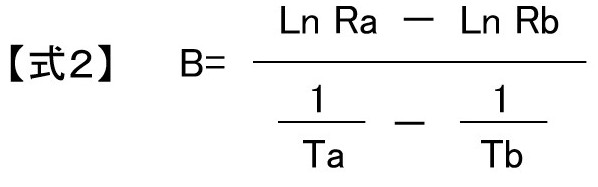
Ta、Tb: 絶対温度 (K)
Ra、Rb: Ta、Tbにおけるゼロ負荷抵抗値 (Ω)
B :B定数 (K)
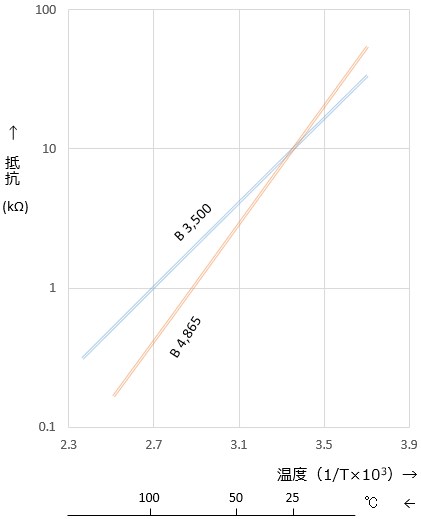
この特性をlogRと1/Tでグラフ化すると、ほぼ直線で表すことが可能です。
B定数は「B25/85」の様に表記され、B25/85であれば25℃と85℃の2点間の抵抗値から算出した値を示します。
B定数は大きいと、グラフの傾きも大きくなるため、小さい温度変化を検知しやすい、温度変化に対し感度が高いということが言えます。
熱放散定数とは、熱平衡状態でサーミスタ素子の温度を、自己発熱によって1℃上げるために必要な電力を表す定数で、サーミスタの消費電力と素子の温度上昇の比で求めます。
サーミスタの消費電力をP(mW)とすると、熱放散定数は式3で求められます。
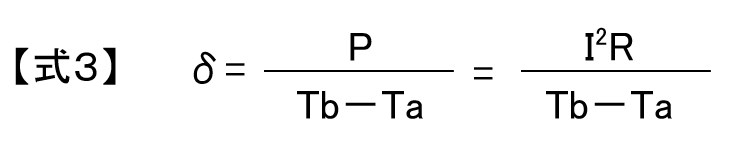
熱放散定数はサーミスタの材料や構造、大きさにより決まります。
またサーミスタを温度測定に使用する際には、測定温度の誤差を生じないように、印加電力を出来るだけ小さくするのが望ましいです。
熱時定数とは、ゼロ負荷の状態でサーミスタの周囲温度を急変させたとき、サーミスタの素子の温度が最初の温度と最終到達温度との温度差の63.2%変化するのに要する時間を表す定数です。
熱時定数(τ)をn倍したときの温度差の変化率は以下のようになり、
熱時定数の約3倍の時間で、温度差の95%変化することとなります。
τ=63.2% 2τ=86.5% 3τ=95.0%
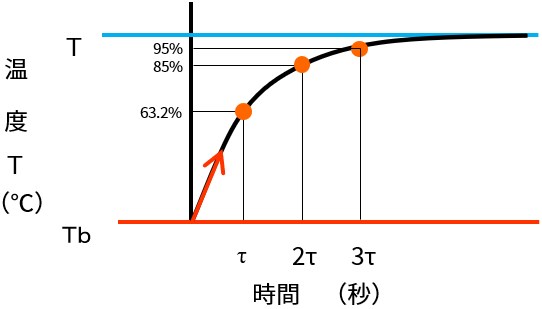
熱時定数が小さくなるほど、温度変化に対する応答速度が速くなります。
